Коллекторское агентство «Феникс», которое судится с омичами, проиграло процесс | Последние Новости Омска и Омской области
«Все 30 платежек агентства имеют очевидные признаки подложности» — заявил юрист.
Коллекторское агентство «Феникс» усердно судится с омичами — только в Куйбышевском райсуде Омска на этой неделе от него рассматривается шесть исков.
Между тем «Феникс» не всегда использует законные документы — об этом сообщила на днях юридическая социальная сеть 9111.ru.
В том числе и по этой причине суд отказал коллекторам в удовлетворении иска о взыскании задолженности по кредитному договору.
Осенью 2021 года ООО «Феникс» обратилось в Протвинский горсуд Московской области с иском о взыскании с клиентки банка «Ренессанс Кредит» Анастасии С. задолженности по договору о выпуске и использовании кредитной карты.
В подтверждение выдачи девушке кредита «Феникс» представило выписку по счету и 30 платежных ордеров.
— На первый взгляд, платежные ордера могли показаться действительными, так как имеется отметка об исполнении платежей. Однако при их детальном исследовании одного из них выяснилось, что время выполнения ордера не соответствует указанной в нем дате (2014 год), так как БИК 044525135 и к/сч 30101810845250000135 используются банком только с 14 июня 2016 года, что подтверждается объявлением на официальном сайте банка в интернете, — объяснил юрист Степан Солдат.
Очевидные признаки подложности, сообщил юрист, имели все 30 платежных ордеров. Неверными в них оказались и другие данные:
— В платежных ордерах указана форма по ОКУД 0401060. Однако, согласно положению Банка России от 19 июня 2012 года № 383-П «О правилах осуществления перевода денежных средств» (действовало до 18 сентября 2021 года), форма — по ОКУД платежного ордера 0401066.
Более того, во всех платежных ордерах в графах «Плательщик» и «Получатель» указан один и тот же счет, что говорит об отсутствии движения денежных средств по счету.
Все это юрист изложил в возражении на иск.
Вдобавок суд установил, что коллекторы пропустили срок исковой давности.
Анастасия С. пояснила суду, что действительно брала в банке кредит, но давно его погасила.
В результате в конце 2021 года суд отказал «Фениксу» в удовлетворении исковых требований.
Степан Солдат сожалеет, что в мотивировочной части решения суд не указал причины, по которым отверг платежные ордера, имеющие явные признаки подложности. Там лишь говорится, что коллекторское агентство не предоставило надлежащих и бесспорных доказательств образования задолженности по кредитному договору.
Вообще же, подытожил юрист, на что только некоторые банки не идут: подделывают банковские, расходные и мемориальные ордера, платежные поручения.
На своей страничке юридической соцсети Солдат приводит подробные примеры таких подделок (подробности — ЗДЕСЬ). Но добавляет, что вовсе не призывает отказаться от платежей по кредитам. Его цель — повышение грамотности потребителей финансовых услуг.
Мария Мельникова
Delta 8 Carts — eileen_griselda — Игры — Gamer.ru: социальная сеть для геймеров
Delta 8 Vape Juice Review — Overall Best D8 Cartridges on the Market
The Delta 8 brand has a loyal following among cannabis smokers, but is it worth the money? This vape juice has a lot of potential for people who are just getting started with cannabis. On Area 52’s website, you can find that it has an easy navigation and aims to appeal to the sophisticated highbrow customer. While it may not be the cheapest option, it delivers a premium product and delicious exotic flavors that make for an enjoyable and quality experience.
The taste of Delta 8 is unmatched by any other vape juice. It is a natural hemp oil made from organic and fair-trade ingredients and is sourced from the US. This product is also incredibly affordable, with free shipping when you spend more than $50. Just make sure you check the price, as small bottles are more expensive. Moreover, smaller bottles are better than 30ml bottles because they are less likely to evaporate.
They also last longer, as less oxygen can reach the e-liquid, which is why you’ll be able to get more out of your purchase.
The taste of Delta 8 products is unmatched and the benefits are numerous. As with any other vape juice, you can try them in small doses to get the most out of the flavor. To make sure you don’t experience unpleasant side effects, you can always order a sample pack or two. Once you’ve tried a few, you can gradually increase the dosage as desired. You can also check out the reviews online to determine whether or not they’re the right choice for you.
If you’re new to vaping, Delta 8 is best tried at a store. If you’re not sure what to expect, you can also try it by smoking a joint. The vape juice is less potent than other cannabis products and is great for first-timers. Besides, stores that sell this brand have excellent customer service, so it’s better to get a sample first before committing to purchasing.
The Delta 8 vape juice contains a high concentration of THC. It is best to start with a low-quality product. It may not be as good as you’d like. However, it’s safe to use it for long-term use. Its flavor is not as strong as that of regular CBD. It also doesn’t have the same effect as D-9. You can purchase a high-quality cartridge that has a PG/VG base for the best vape experience.
For newbies, it’s important to increase the dosage slowly to get the right effect. For example, you may find that 15 mg is not enough at first. If you’re using it regularly, you may want to consider increasing your dosage by five to fifteen milligrams per week. Increasing dosage slowly helps prevent the development of a tolerance. Regardless of your preference, you’ll be happy with the results.
Related article: Delta 8 Gummies Cost — How Much Do They Cost?
Социальная направленность политики государства расширяется
Сохранению стабильных цен способствуют различные механизмы. За сдерживанием инфляционных процессов следят местные органы власти, профсоюзы, МАРТ, Комитет государственного контроля.
С понедельника в Беларуси действует соглашение о скидках на социально значимые товары для уязвимых категорий населения. Кому и на какие товары положены льготы?Экономия на кассе
Заглядываю в магазин возле дома. Местные жители активно выбирают хлеб и молочные товары. Немало покупателей и в мясном отделе.— Закупаюсь обычно на пару дней, — признается бабушка, изучая ассортимент на полках. — Сегодня решила взять белорусский картофель по 1 рублю 65 копеек за килограмм, творог, молоко. Предпочитаю обычные магазины, которые находятся недалеко от дома. Выбор хороший, часто бывают акции. Пусть и небольшая, но скидка для пенсионеров предоставлялась и раньше. А на этой неделе переоформила карту на «Е-плюс. Социальная», чтобы экономия стала более существенной.
С понедельника торговые сети начали оформлять специальные бонусные карты. Чтобы такую получить, необходимо предоставить копию документа, который подтверждает право на скидку. Ей могут воспользоваться пенсионеры, многодетные семьи, инвалиды и семьи, воспитывающие ребенка-инвалида до 18 лет, а также получатели социального пособия.
В каждой из торговых сетей свои нюансы предоставления льгот. Например, у одного из ретейлеров покупателям, которым уже были положены бонусы, предложили сделать выбор — пользоваться прежним вариантом скидки на весь ассортимент в размере 3 % или подключиться к новой программе, которая помогает уменьшить расходы на 10 % на социально значимые товары. В другом месте за 1 копейку нужно приобрести специальную карту и зарегистрироваться на сайте компании для участия в программе лояльности.
Цены на контроле
Кстати, по данным Продовольственной и сельскохозяйственной организации ООН, за прошлый год продукты питания в мире подорожали на 28,1 %, то есть почти на треть. Такая ситуация оказывает влияние на рост цен в Беларуси. По итогам года инфляция на внутреннем рынке у нас составила 9,97 %, на социально значимые товары — около 9 %.В этих условиях государство приняло беспрецедентные меры, чтобы сдержать инфляционные процессы. Масштабное соглашение заключено Министерством антимонопольного регулирования и торговли с Ассоциацией розничных сетей и субъектами торговли о предоставлении скидки в размере 10 % на определенные группы социально значимых товаров.
Ответственность бизнеса
Галина Лагунова, заместитель председателя Постоянной комиссии Палаты представителей Национального собрания по экономической политике, уверена, что принятие данного соглашения — прямая и непосредственная помощь со стороны государства людям, которые по различным обстоятельствам оказались в тяжелом материальном или социальном положении:По словам Галины Лагуновой, необходима высокая степень вовлеченности компании в жизнь общества — бизнес должен быть социально ответственным. Некоторые сети устанавливают нулевую и даже отрицательную торговую наценку на продукты питания за счет собственной маржи, так как более низкая конечная цена на социально значимые товары и продукты питания помогает выиграть конкурентную борьбу за покупателей. Также парламентарий отметила, что рост цен будет не столь болезненным, если полностью или частично компенсировать его увеличением зарплат. Возможности для их роста связаны с наращиванием объемов производства, то есть производительности труда в национальной экономике.
Бережное, внимательное отношение к запросам людей проявляется не только в ценовой политике. Например, в Беларуси создана масштабная система социальной защиты пенсионеров, инвалидов, других уязвимых слоев населения. Речь о льготах на проезд, возможности оплачивать жилищно-коммунальные услуги по субсидируемым тарифам, освобождении от налога на недвижимость и землю, скидке на оплату некоторых нотариальных услуг и многом другом. Это касается государственной политики.
Но не менее важно развивать механизмы привлечения юридических лиц и индивидуальных предпринимателей к реализации соцпроектов.
МНЕНИЯ
Михаил Ковалев, экономист:
— Цены на товары первой необходимости должны быть справедливыми. В непростых условиях были приняты своевременные меры — данное соглашение в интересах населения поможет сдержать инфляционные процессы. Важно, чтобы при нестабильности на внешних рынках каждый, независимо от уровня достатка, мог купить товары повседневного спроса. Но на мой взгляд, необходимо четко объяснить покупателям, как получить скидку, какие для этого необходимы документы, в какое время она будет действовать. Сейчас у каждой торговой сети действуют свои карты лояльности, возможно, для удобства есть смысл введения единого социального удостоверения.
Алеся Сикора, пенсионерка:
— Инициатива с введением скидок для уязвимых категорий населения важна и своевременна. Уверена, идея должна найти продолжение и в сети аптек.
Частным аптекам необходимо быть более гибкими в вопросе формирования цены. Особенно по востребованным сегодня лекарствам.
Елена Голубева, начальник главного управления по культуре и общественной работе Федерации профсоюзов:
— Профсоюзы на постоянной основе оказывают помощь людям, которые ушли на заслуженный отдых. Большинство коллективных договоров содержит положения по оказанию всесторонней поддержки ветеранам. Среди них материальные выплаты и подарки к юбилеям, профессиональным и другим праздникам, помощь в оздоровлении и лечении, заготовка продуктов на зиму, доставка топлива, обработка приусадебных участков и многое другое.
Биатлон — всё от КМ и ЧМ до соревнований Кубка России и IBU
Сезон в России и мире
| Норицын о Резцовой: «Сейчас хорошие скорости, но она может стать быстрее» |
Бывший тренер женской сборной России Виталий Норицын, который сейчас работает с командой Болгарии и помогает Кристине Резцовой, ответил на вопросы корреспондента «Матч ТВ» Михаила Кузнецова. |
| Сборная России — серебряный призер в мужской эстафете 7 этапа КМ в Италии! |
Сегодня, 23 января, сильнейшие стреляющие лыжники планеты разыграли последний комплект наград КМ-2021/2022 перед Олимпиадой в китайском Пекине. Победителями в мужской эстафетной гонке на итальянском этапе Кубка мира стали норвежские… |
| Кристина Резцова — четвертая в масс-старте 7 этапа Кубка мира в Антхольце |
В воскресенье, 23 января, в Антхольц-Антерсельве завершился последний перед Зимней Олимпиадой в Китае этап Кубка мира-2021/2022. Программу итальянского турнира закрыла гонка с общего старта у представительниц слабого пола. Победу… |
| Дарья Виролайнен отмечает сегодня свой день рождения! |
Дарья, желаем, чтобы путь к победам стал легче, пусть приятные, яркие моменты и повороты судьбы сопровождают Вас в дальнейшем! Верьте, стремитесь, надейтесь, любите, будьте здоровы, красивы, успешны и счастливы! Продолжайте дарить. |
| Мужская серебряная эстафета 7 этапа КМ |
Какая нынче эстафета! Чем так и славен биатлон. Такую яркость дать сюжету Мечтает каждый чемпион. Ничто парней не удержало: Поломки, промахи, раскат, И даже круг штрафной в финале Не смог испортить результат. Все героически… |
| Состав сборной России на чемпионат Европы в немецком Арбере |
Союз биатлонистов России (СБР) огласил имена спортсменов, которые отправятся выступать на чемпионат Европы-2022. Турнир пройдет в немецком Арбере в период с 26 по 30 января. В состав команды вошли Бабиков, Поварницын, Шевченко и … |
| Россиянки завоевали серебряные медали в эстафете на 7 этапе КМ с тремя штрафными кругами! |
В субботу, 22 января, в итальянском Антхольце в рамках седьмого этапа Кубка мира сильнейшие представительницы слабого пола разыграли награды в финальной эстафетной гонке на КМ перед Олимпиадой в китайском Пекине. |
| Михаил Шашилов: «Иностранные коллеги говорят, что у нас команда будущего» |
Комментарии после призовой эстафеты Валерии Васнецовой и Михаила Шашилова, катание на горных лыжах в Тоблахе. |
| Бабиков: «Надо пахать и никогда не опускать руки. Стараюсь видеть только позитив» |
Антон Бабиков объяснил, что случилось в эстафете на 7 этапе КМ, когда он бежал какую-то часть дистанции без одной палки. «Соперник наступил мне на палку, полностью слетела «лапка», он полностью снял её. Я ехал на спуске и махал палкой… |
| Антон Бабиков выиграл «индивидуалку» на 7 этапе КМ в Антхольце! Карим Халили — третий! |
В четверг, 20 января, в Антхольц-Антерсельве стартовал последний этап мирового Кубка перед главным стартом четырехлетия, Олимпиадой. |
| Все Новости » |
Полный текст интервью читайте в первоисточнике…
..
Золотые медали с…
Программу итальянского этапа открыла индивидуальная гонка у представителей сильного пола. В 20 км…ЧЕ-2022, Арбер (Германия), 26-30 января
26 января (среда)
12:15 индивидуальная гонка, мужчины
16:00 индивидуальная гонка, женщины
28 января (пятница)
12:30 спринт, мужчины
16:00 спринт, женщины
29 января (суббота)
12:30 преследование, мужчины
15:30 преследование, женщины
30 января (воскресенье)
12:30 смешанная эстафета
15:30 супермикст
6 этап IBU Cup, Нове Место (Чехия), 3-5 февраля
3 февраля (четверг)
12:30 спринт, женщины
16:00 спринт, мужчины
5 февраля (суббота)
12:30 спринт, женщины
16:00 спринт, мужчины
ОИ-2022, Пекин (Китай), 5-19 февраля
5 февраля (суббота)
12:00 смешанная эстафета
7 февраля (понедельник)
12:00 индивидуальная гонка, женщины
8 февраля (вторник)
11:30 индивидуальная гонка, мужчины
11 февраля (пятница)
12:00 спринт, женщины
12 февраля (суббота)
12:00 спринт, мужчины
| № | Мужчины | Страна | Очки |
| 1 | Norway | NOR | 5165 |
| 2 | Russia | RUS | 5061 |
| 3 | France | FRA | 5001 |
| 4 | Germany | GER | 4774 |
| 5 | Belarus | BLR | 4208 |
| 6 | Sweden | SWE | 3949 |
| 7 | Ukraine | UKR | 3905 |
| 8 | Italy | ITA | 3876 |
| 9 | Austria | AUT | 3434 |
| 10 | Switzerland | SUI | 3371 |
| полная таблица | |||
| № | Женщины | Страна | Очки |
| 1 | France | FRA | 5029 |
| 2 | Sweden | SWE | 4802 |
| 3 | Norway | NOR | 4745 |
| 4 | Russia | RUS | 4602 |
| 5 | Belarus | BLR | 4498 |
| 6 | Germany | GER | 4477 |
| 7 | Czech Republic | CZE | 3933 |
| 8 | Italy | ITA | 3889 |
| 9 | Ukraine | UKR | 3755 |
| 10 | Austria | AUT | 3492 |
| полная таблица | |||
Биатлон сегодня — это наиболее популярный, зрелищный, зимний вид спорта.
Чемпионат и Кубок мира смотрят миллионы людей всех возрастов и статусов и с нетерпением ждут начала трансляций каждого этапа КМ. Спортивная международная пресса уделяет пристальное внимание этому олимпийскому двоеборью, а его популярность в мире ярко отражает рост интереса к лыжам и лыжному спорту. Об этом же свидетельствует увеличение количества фан-клубов, различных соревнований, специализированных школ, информационных ресурсов, освещающих новости этого спорта, расширение программы Олимпийских игр, чемпионатов мира и растущий с каждым годом список стран-участниц. С момента решения о проведении в России Зимних Олимпийских Игр повышенное внимание к развитию этого спорта многократно усилилось!
Россия является одной из стран лидеров современного биатлона. Но чемпионаты мира и соревнования на этапах КМ, прошедшие после Олимпиады, показали, что наши спортсмены далеки от идеальной спортивной формы, российская школа уже не имеет громадного преимущества, которое было во времена СССР и прежние годы.
Последние ЧМ успешно прошли, задачи поставленные перед российской командой выполнены, у нашей сборной есть медали, но то нет ни одной золотой награды в личных соревнованиях, то нет наград в эстафетах. В новом сезоне у нашей сборной новая команда, у тренерского штаба еще есть время для экспериментов, т.к. в олимпийском сезоне придется решать сложнейшие задачи и формировать сборную на ОИ-2022, которая пройдет в китайском Пекине. А нам, болельщикам, остается только всеми силами поддерживать и болеть за наших! Cезон КМ 2021-2022 обещает быть очень эмоциональным!
Мы всегда открыты и готовы к сотрудничеству!
Официальный сайт всегда открыт для Вас и готов опубликовать Вашу информацию, новости, поднять интересующие Вас вопросы, выслушать и выполнить Ваши пожелания и предложения! Наша спортивная социальная сеть всегда рада добрым, интересным, позитивным людям! Мы приглашаем спортсменов, тренеров, болельщиков и фанатов всех стран, средства массовой информации и журналистов, спортивные секции и школы, организаторов соревнований и руководителей, спонсоров и благотворителей принимать активное участие в развитии спорта!
Биатлон — это поистине наш национальный зимний вид спорта.
Очень приятно, что Вы и огромная аудитория людей нашей страны интересуетесь этим прекрасным спортом. Мы верим, что здоровье нации, напрямую зависит от пропаганды здорового образа жизни и интерес к спорту это уже вклад в его развитие. Развитие спорта в стране и его престиж на мировой арене зависят ОТ НАС, нас вместе. Вместе мы сможем преодолеть все сложности и достичь необыкновенных высот!
Пишите нам и мы обязательно ответим и поможем!
По результатам почти полувековых самых престижных спортивных баталий на стрельбищах и лыжных трассах советско-российская научно-педагогическая школа бега на лыжах с винтовкой получила международное признание, обрела мировую известность. Рекордные достижения наших атлетов были обеспечены талантом и трудолюбием работающих с ними тренеров, врачей, массажистов, научных работников, сотрудников сервисных групп, руководителей спорта, создателей отечественного комплекса «оружие плюс патрон» — одного из лучших в мире. Великие достижения, победные традиции наших стреляющих лыжников, вклад отечественных специалистов в процветание олимпизма, всего международного спортивного движения — это национальная гордость России!
История этого вида спорта начинается с 1949 года.
Чемпионаты мира ежегодно проводят с 1958 года, а олимпийскую прописку этот спорт получил в 1960 году на VIII Играх в Скво-Вэлли (США). В каждом олимпийском году мировые чемпионаты разыгрывают только в тех дисциплинах, которые не входят в олимпийскую программу. Долгие годы этот спорт был исключительно мужским видом. Соревновательные программы Олимпиад и чемпионатов включали только один вид — лыжную гонку на 20 км со стрельбой из боевого оружия на 4 огневых рубежах, по 5 выстрелов на каждом. Любопытно, что на 1-3-м рубежах стрельбу разрешали вести из любого положения (почти все спортсмены, естественно, отдавали предпочтение положению лежа), а на последнем, 4-м, рубеже — только из положения стоя. За каждый промах ко времени прохождения соревновательной дистанции начисляли еще 2 штрафные минуты.
Раздел сайта для тренеров и специалистов, а также студентов физкультурных ВУЗов, обучающихся по специальности «Физическая культура и спорт», посвящен актуальным вопросам подготовки квалифицированных спортсменов, системам тренировок, специфике соревновательной деятельности, в том числе и членов сборных команд России.
Представленные методологические особенности процесса подготовки разработаны на основе научного подхода, с использованием материалов исследований ведущих специалистов-теоретиков и тренеров-практиков.
определение classmates.com и синонимы classmates.com (английский)
Взято из Википедии, бесплатной энциклопедии
Classmates.com — социальная сеть, созданная в 1995 году [1] Рэнди Конрадсом, который основал Classmates Online , Inc. [2] Веб-сайт социальной сети помогает участникам находить, связываться и поддерживать связь с друзьями и знакомыми на протяжении всей их жизни, включая детский сад, начальную школу, среднюю школу, колледж, работу и армию США.Classmates.com насчитывает более 40 миллионов [3] активных пользователей в США и Канаде. В начале 2008 года Nielsen Online поставила Classmates на третье место среди уникальных ежемесячных посетителей (дома в США, на работе) среди сайтов социальных сетей. [4]
Бизнес-модель
Нейтральность этого раздела оспаривается . Пожалуйста, смотрите обсуждение на странице обсуждения. Пожалуйста, не удаляйте это сообщение, пока спор не будет разрешен. (август 2009 г.) |
Бизнес-модель Classmates Media Corporation основана на пользовательском контенте и доходах от платной подписки и продажи рекламы. [5] Classmates Media насчитывает более 50 миллионов участников, в том числе более 3,8 миллиона платных подписчиков, по состоянию на 30 июня 2008 г. 2008 г. по сравнению с 30 июня 2007 г., а во втором квартале 2008 г. общее количество платежных счетов увеличилось на 288 000 до более чем 3,8 миллиона платежных счетов. [7] В первом квартале 2008 года чистый прирост платных аккаунтов составил рекордные 322 000. [8]
Доходы Classmates Media за второй квартал 2008 года составили 57 долларов.0 миллионов, увеличившись на 19% по сравнению с кварталом прошлого года. [9] В первом квартале 2008 года доходы Classmates Media выросли на 22% до 51,9 миллиона долларов по сравнению с кварталом прошлого года.
[6]
Отчет Ассоциации онлайн-издателей о расходах на платный контент на рынке США, Classmates.com занял 4-е место среди 25 лучших веб-сайтов по доходу от потребительского контента как в 2002, так и в 2003 году [10] (последние годы, когда ранжирование отдельных сайтов было разбито).
Конфиденциальность
Одноклассники.com используют настоящие имена, а не псевдонимы (хотя некоторые участники используют «вымышленное имя»). Конфиденциальность участников защищена двойной слепой системой электронной почты, поэтому адреса электронной почты и контактная информация никогда не раскрываются, если они не раскрываются самими участниками один на один.
Регистрация и общение в сети
Регистрация в качестве базового участника Classmates.com бесплатна. Базовые участники могут создавать профили и искать друзей по всей социальной сети. Базовые участники также могут публиковать и читать доски объявлений сообщества и просматривать информацию о предстоящих встречах, но они не могут никому отправлять электронные письма или просматривать профили других участников.
Они могут писать электронные письма и отправлять их, но получатель не может их читать, если только отправитель не станет платным участником. Это не становится очевидным, пока электронное письмо уже не составлено и не отправлено. Базовые участники, которые пытаются отправлять электронные письма или просматривать профили, перенаправляются на страницу, где они могут перейти на статус Gold за определенную плату. Члены со статусом Gold, которые вносят плату, могут просматривать профили других участников, фотографии, биографии, хронологию, интересы, объявления, а также отправлять электронные письма и получать электронные письма от любого участника, просматривать заметки, размещенные на доске объявлений их профиля, видеть имена других, которые посетили свой профиль и подписали свою гостевую книгу, получили доступ и использовали инструменты для планирования встреч и создали свои собственные частные группы.
Собственность
Нейтралитет этого раздела оспаривается . Пожалуйста, смотрите обсуждение на странице обсуждения. Пожалуйста, не удаляйте это сообщение, пока спор не будет разрешен. (август 2009 г.) |
Classmates Media управляет ведущими онлайн-сервисами социальных сетей и маркетинга лояльности в рамках Classmates.com [12] и бренды MyPoints [13] . Classmates.com связывает миллионы участников в США и Канаде с друзьями и знакомыми из школы (K-12), колледжа, работы и армии. Classmates Media также управляет сайтом номер один в Германии для воссоединения со школьными друзьями, StayFriends.de. [14] [15] , а также StayFriends.se [16] крупнейший сайт в Швеции для воссоединения со школьными друзьями. [17] Ведущие сайты социальных сетей Classmates Media также включают StayFriends.
по телефону [18] в Австрии и Trombi.com [19] во Франции.
Спорная деловая практика
Стандартной практикой Classmates.com является автоматическое продление членства в конце каждого расчетного периода. В декабре 2006 года, когда журнал PC World протестировал несколько компаний, чтобы определить, насколько легко или сложно было отказаться от их услуги, Classmates.com была одной из компаний, получивших худший рейтинг. [20]
Classmates.com также регулярно рассылает электронные письма о том, что один из одноклассников получателя ищет его/ее.Утверждается, что это часто не соответствует действительности, и Classmates.com в настоящее время сталкивается с судебным иском за эту практику (которая, если утверждение верно, представляет собой мошенничество). [21] Кроме того, Classmates.com не позволяет участникам предоставлять друг другу частные адреса электронной почты, поскольку это позволило бы участникам общаться друг с другом за пределами сайта и, следовательно, не платить за общение.
United Online, материнская компания Classmates.com, заработала 70 миллионов долларов на маркетинговых методах, которые в 2009 году расследовал Сенатский комитет по торговле, включая совмещение второй транзакции по кредитной карте с членством в Classmates. Грег Сандовал (23 ноября 2009 г.). «Интернет-магазины, пойманные на маркетинговом« мошенничестве », обвиняют клиентов» . Cnet.com. http://news.cnet.com/8301-1009_3-10403286-83.html. Проверено 22 августа 2009 г. .
Внешние ссылки
Предикторы точного восприятия отношений одноклассников
Точное восприятие отношений
Сетевые исследования точного восприятия отношений имеют долгую историю, восходящую к влиятельной серии исследований, проведенных Бернардом, Киллвортом и Сэйлором (BKS) (см. обзор Bernard, Killworth, Kronenfeld, & Sailor, 1984).Исследования точности BKS были сосредоточены на сообщениях взрослых об их собственном общении с другими, и было обнаружено, что «то, что люди говорят об их общении, не имеет никакого полезного сходства с их поведением» (Bernard et al.
, 1984; стр. 499). С тех пор как эти исследования были опубликованы, другие утверждали, что, хотя люди изо всех сил пытаются сообщить о конкретных взаимодействиях, они могут быть более точными в своих воспоминаниях о долгосрочных устойчивых моделях общения (например, Freeman, Romney, & Freeman, 1987).
Эти первоначальные исследования точности отчетов взрослых об их собственных взаимодействиях побудили сетевых исследователей начать изучение точности отчетов взрослых об их взаимодействиях и отношениях.В частности, Крэкхардт (1987) разработал когнитивные социальные структуры (CSS) как метод оценки восприятия людьми всей сетевой структуры в обстановке, утверждая, что восприятие, а не фактическая сетевая структура, может быть более важным фактором, определяющим поведение. Например, Крэкхардт и Килдафф (1999) отмечают, что «восприятие социальной сети… помогает определить, предпринимает ли человек действие и насколько эффективным может быть это действие. Структура отношений может как способствовать, так и ограничивать действие, и эта социальная структура опирается на лежащую в основе модель восприятия в сознании людей» (с.
770). То есть, в соответствии с феноменологической точкой зрения (Bronfenbrenner, 1979), люди действуют, основываясь на своем собственном, часто несовершенном, восприятии социальных отношений в данной среде. Кроме того, и, возможно, что более важно, точность восприятия социальных отношений является ключом к способности людей вести себя таким образом, который приводит к желаемому эффекту или результату (Krackhardt, 1990). Например, Майя может захотеть подняться по социальной лестнице в своем классе и может заметить, что у Бритни много друзей.Основываясь на этом восприятии, она может попытаться подружиться с Бритни. Такое поведение, по мнению Майи, будет более эффективным для достижения ее цели (т. е. подъема по социальной лестнице), если у Бритни действительно много друзей.
CSS предоставляет гибкие методы оценки индивидуальной точности в сравнении с подтвержденными отношениями, о которых сообщают сами люди (т.г., Бондонио, 1998; Бренды, 2013; Крэкхардт, 1987). Исследования CSS взрослых в основном были сосредоточены как на предикторах, так и на результатах точности наблюдателя, а не цели, в восприятии отношений.
Например, в исследованиях изучалось, как такие аспекты, как центральное место в сети, восприятие власти, демография и личностные черты, связаны с точностью наблюдателя структуры социальной сети на рабочих местах или в сетевых экспериментах (например, Bondonio, 1998; Casciaro, 1998; Casciaro, Carley, & Krackhardt, 1999; Simpson, Markovsky, & Steketee, 2011).Более того, в соответствии с идеей о том, что точное восприятие может дать более эффективные результаты, дополнительные исследования взрослых показали, что точность наблюдателя социальных отношений связана с такими преимуществами, как лидерство, власть и положительные результаты работы (например, Balkundi & Kilduff, 2006; Кракхардт, 1990).
По сравнению с исследованиями взрослых литература о восприятии детьми отношений со сверстниками в классе более ограничена и сосредоточена исключительно на предикторах, а не на результатах точности наблюдателя (например,г., Капелла, Нил и Саху, 2012 г.; Нил, Нил и Капелла, 2014 г.). Это предыдущее исследование восприятия детьми отношений между одноклассниками было сосредоточено на том, как ситуационные характеристики (например, размер класса, эмоциональная поддержка учителя) и атрибуты наблюдателя (например, класс, пол) влияют на точность наблюдателя (Cappella et al.
, 2012). Как и в исследованиях взрослых, в исследованиях восприятия детьми отношений со сверстниками в классе еще не учитывались факторы, влияющие на точность цели. Кроме того, в предыдущей работе (Cappella et al., 2012; Neal et al., 2014) еще не рассматривал роль социального статуса как предиктора правильного восприятия одноклассниками отношений со сверстниками. Восприятие сверстников как популярного может быть связано с повышенной точностью наблюдателя, но также может повлиять на точность цели. То есть может быть легче увидеть отношения между одноклассниками, которых считают популярными в классе.
Помимо теоретических и эмпирических мотивов, изучение точности восприятия детьми отношений одноклассников имеет важное методологическое значение для измерения и моделирования сети.Во-первых, это может помочь уточнить методы оценки взаимоотношений детей в классе, включая социально-когнитивное картирование (Cairns & Cairns, 1994) и когнитивные социальные структуры (Neal, 2008). Эти методы обычно триангулируют ответы группы наблюдателей сверстников, чтобы измерить структуру отношений в классе или классе.
Однако каждый наблюдатель и каждое сообщаемое взаимоотношение считаются одинаково точными. Изучение различий в точном восприятии детьми отношений со сверстниками может помочь определить, могут ли усовершенствования этих подходов привести к более точным измерениям.
Во-вторых, исследуется критическое допущение стохастических моделей, основанных на акторах (Snijders, van de Bunt, & Steglich, 2010), которые становятся все более популярными в социальных исследованиях для распутывания эффектов отбора и влияния. В конкретном контексте психологии развития эти модели использовались для изучения формирования сетей среди детей дошкольного возраста (например, Schaefer, Light, Fabes, Hanish, & Martin, 2010; Martin, Kornieko, Schaefer, Hanish, Fabes, & Goble, 2013). ), этнической сегрегации в среднем детстве и подростковом возрасте (Leszczensky & Pink, 2015), и недавно использовались в 15 статьях, опубликованных в специальном выпуске по сетевой динамике в Journal of Research on Adolescence (см.
Veenstra, Dijkstra, Steglich, & Ван Залк, 2013).Однако, в зависимости от типов оцениваемых эффектов, эти модели требуют допущения о том, что участники сети обладают определенным уровнем точной информации о сети, начиная от «полной информации о структуре и составе сети» (Veenstra et al., 2013, p. 402) до «более ограниченной информации» (Snijders et al., 2010, стр. 46). Изучение вариаций и предикторов точного восприятия детьми отношений со сверстниками может помочь понять, когда эти предположения выполняются, и серьезность их потенциального нарушения.
Предикторы точного восприятия отношений в детстве
Многие различные факторы могут быть связаны с точностью восприятия детьми отношений. Здесь мы сосредоточимся на четырех факторах, для которых было достаточно прошлых исследований, чтобы разработать конкретные, проверяемые гипотезы.
Класс
Изменения в развитии могут повысить точность восприятия наблюдателем отношений между одноклассниками, то есть способность ребенка видеть отношения.
По мере развития детей у них улучшается социальное познание, что увеличивает их способность к точному межличностному восприятию (Cillessen & Bellmore, 2011; Dodge & Price, 1994).В школьных исследованиях уровень класса часто используется в качестве косвенного показателя для оценки влияния на развитие. Эти исследования показывают, что дети в старших классах точнее оценивают, как их собственный социальный статус, поведение и способности воспринимаются сверстниками (Ausubel, Schiff, & Gasser, 1952; Malloy, Yarlas, Montevilo, & Sugarman, 1996; Malloy et al. др., 2007). Дети в старших классах также в большей степени согласны с мнением одноклассников о наличии отношений со сверстниками в классе (Cappella et al., 2012). Таким образом, мы предполагаем, что дети в старших классах будут иметь более точное представление об отношениях своих одноклассников ( h2A ).
Изменения в развитии также могут повысить точность определения цели (например, пары детей, которых видят другие).
По мере того, как дети становятся старше, у них, как правило, более стабильные отношения (например, Cairns, Leung, Buchanan, & Cairns, 1995; Gifford-Smith & Brownell, 2003). Это повышение стабильности должно облегчить точное наблюдение за отношениями одноклассников в старших классах, что отражается в повышенной точности в отношении целей.Таким образом, мы предполагаем, что отношения между парами детей в старших классах будут восприниматься точнее ( h2B ).
Размер класса
Размер класса также может иметь значение для точного восприятия взаимоотношений одноклассников. Поскольку количество возможных диад увеличивается геометрически с размером класса (например, диады = (размер 2 — размер)/2), даже небольшое увеличение размера класса резко увеличивает количество диад, которые дети должны пытаться наблюдать.В таких многолюдных местах наблюдателям может быть трудно увидеть отношения, а цели могут быть не видны, что снижает точность как наблюдателя, так и цели.
В соответствии с этим предыдущие исследования показали, что дети в больших классах меньше соглашались с мнением сверстников о наличии отношений в классе (Cappella et al., 2012). Таким образом, мы предполагаем, что дети в небольших классах будут иметь более точное восприятие отношений между одноклассниками ( h3A ) и что отношения между парами детей в небольших классах будут восприниматься более точно ( h3B ).
Пол
В среднем детстве девочки и мальчики различаются в своих социальных познаниях, что может повлиять на их точность в качестве наблюдателей за отношениями со своими одноклассниками. В частности, девочки, как правило, демонстрируют ориентированные на отношения социальные познания, такие как эмпатия и цели поддержания социальных связей. Напротив, мальчики, как правило, проявляют агентные социальные познания, такие как цели сохранения собственного социального статуса (см. обзор Rose & Rudolph, 2006). Однако, несмотря на эти различия в социальном познании, исследования гендерных различий в точности межличностного восприятия были неоднозначными (Cillessen & Bellmore, 2011).
Некоторые исследования показали, что девочки демонстрируют более точное восприятие собственных или чужих компетенций и социального статуса, чем мальчики (например, Cillessen & Bellmore, 1999; LaFontana & Cillessen, 1999; Smith, Van Gessel, David-Ferdon, & Kistner, 2013). ), в то время как другие обнаружили незначительные или ограниченные половые различия (например, Malloy et al., 1996; 2007). Кроме того, в то время как Cappella et al (2012) обнаружили, что девочки демонстрируют более высокий уровень согласия с консенсусом сверстников в отношении наличия отношений в двумерном анализе, они не обнаружили гендерных различий в иерархической линейной модели, которая контролировала другие индивидуальные и классные эффекты. .Эти смешанные результаты в литературе, вероятно, отражают различия в выборке и измерении межличностного восприятия, и необходимы дополнительные исследования, чтобы определить, влияет ли пол на точность наблюдателя.
Пол также может влиять на точность прицеливания. В частности, гендерный состав целевой диады может сделать отношения между ними более легкими или трудными для наблюдения.
Среднее детство характеризуется сильной тенденцией детей вступать в группы, сегрегированные по половому признаку, явление, подчеркнутое в теории гендерного развития двух культур (Maccoby, 1990; 1998).Более того, уже в дошкольном возрасте у детей формируется социальное представление о том, что их сверстники предпочитают однополых партнеров по играм (Martin, Fabes, Evans, & Wyman, 1999). Действительно, к среднему детству дети склонны переоценивать важность сходства полов, делая выводы о существовании отношений между одноклассниками (Neal et al., 2014). Поскольку дети склонны проявлять сильные ожидания и предубеждения в отношении однополых отношений в среднем детстве, отношения легче наблюдать между однополыми парами одноклассников.Таким образом, мы предполагаем, что более точно будут восприниматься отношения между парами однополых детей ( h4 ).
Воспринимаемая популярность
Социальный статус в классе может принимать различные формы и может зависеть от того, насколько ребенок нравится сверстникам (т.
е. от социометрического статуса) или от того, насколько популярным воспринимается ребенок сверстниками (т. е. от воспринимаемой популярности) ( например, Coie, Dodge, & Coppotelli, 1982; Parkhurst & Hopmeyer, 1998). В этой статье мы уделяем особое внимание связи между воспринимаемой детьми популярности и точным восприятием отношений в классе.В отличие от социометрического статуса воспринимаемая популярность связана с усиленным социальным контролем и навыками, которые позволяют детям эффективно манипулировать социальными отношениями (Badaly et al., 2012; Cillessen & Bellmore, 2011). Таким образом, дети, которые более точно воспринимают отношения одноклассников (навык, повышающий способность манипулировать социальными отношениями), могут лучше продвигать свою популярность. Дети, которых считают популярными, также обычно занимают хорошие позиции в социальной иерархии класса (Cillessen & Bellmore, 2011; Lease, Musgrove, & Axelrod, 2002).Такое позиционирование может дать популярным детям преимущество в точном наблюдении за отношениями одноклассников.
Основываясь на этой литературе, мы предполагаем, что дети с более высоким уровнем воспринимаемой популярности будут иметь более точное представление об отношениях с одноклассниками ( h5A ).
Воспринимаемая популярность также может быть связана с точностью относительно цели. Поскольку популярные дети находятся на вершине социальной иерархии, их отношения могут быть более заметными и легко наблюдаемыми.Например, дети и ранние подростки часто описывают популярных сверстников как обладающих многими социально заметными характеристиками, такими как атлетизм, привлекательность и крутость (LaFontana & Cillessen, 2002; Lease, Kennedy, & Axelrod, 2002; Rodkin, Farmer, Pearl, & Van Acker). , 2006; Се, Ли, Буше, Хатчинс и Кэрнс, 2006). Поскольку популярные сверстники могут быть более заметными в обществе, что делает их мишенями, которые легко увидеть, мы предполагаем, что отношения между парами детей с более высокими средними воспринимаемыми показателями популярности будут восприниматься более точно ( h5B ).
Точно так же, поскольку дети с большей вероятностью присоединяются к сверстникам с аналогичным статусом (Farmer et al., 2009), отношения между сверстниками с аналогичным уровнем предполагаемой популярности могут соответствовать ожиданиям наблюдателя. Таким образом, мы предполагаем, что отношения между сверстниками с одинаковым уровнем предполагаемой популярности будут восприниматься более точно ( h5C ).
Теория графов
Вероятно, это не первый ваш курс социологии; но даже если это так, отношения относительно интуитивны для людей.Они повсюду вокруг нас: вы и ваши родители, вы и ваши братья и сестры, ваши братья и сестры и ваши родители, вы и ваши одноклассники, ваши одноклассники друг другу. Принадлежность, общение, дружба, ненависть: таково содержание социальных отношений. У двух людей либо есть какие-то отношения, либо нет. По сути, отношения — это связь между по крайней мере двумя социальными акторами. Мы увидим, что иногда, когда отношения объединяются в сети, два набора отношений могут иметь различное содержание, но все же иметь одну и ту же форму (т.
г., расположение или образец).
Технический термин социальных сетей для обозначения «отношений, объединяющихся в сети» — конкатенация . Например, каждый раз, когда вы представляете друг другу двух ранее не связанных друг с другом знакомых, вы объединяете две ранее не связанные связи в связанную тройку.
Например, если вы читаете это, вы, вероятно, зарегистрированы в классе социальной сети, и у вас есть знакомые, такие как ваши друзья и люди, с которыми вы посещали предыдущие занятия, а также люди, которых вы никогда раньше не видели.Может быть очевидно, что у вас есть отношения с теми людьми, которых вы знаете, но есть ли у вас отношения с теми, кого вы не знаете?
Рисунок 2.1: Первое изображение социальной сети, которое тогда называлось «социограммой», было нарисовано Джейкобом Морено в 1934 году. Оно состояло из отношений между 19 мальчиками (треугольники) и 18 девочками (круги) в классе 5-го класса.
Возможно. Это зависит от того, как вы определяете термин социальные отношения.
Если бы вас спросили, кто ваши друзья, вы бы сказали мне, что некоторые из ваших одноклассников — ваши друзья, а остальные — нет.Однако, если бы вас спросили, кто из этих людей в вашем классе является вашим одноклассником, все были бы вашими одноклассниками, кроме вашего профессора или ассистентов преподавателя. Вы разделяете определенный тип отношений с этими другими людьми, вашими одноклассниками, даже если вы никогда не встречались с ними. Слово «одноклассник» даже подразумевает тип отношений, имеющий иное социальное значение, чем «друг». При анализе социальной сети важно сначала понять, какой тип социальных отношений вы анализируете, поскольку это напрямую связано с тем, какие выводы или обобщения вы можете сделать о социальном мире.
Если у вас есть тип социальных отношений, который вы хотели бы изучить, следующим шагом будет привязка контекста. Если вы хотите составить карту всех социальных отношений в мире, это невозможно. Представьте, как сложно было бы составить карту всех людей в вашей школе, которые дружат друг с другом.
Это может быть осуществимо, если у вас всего 1000 студентов, но в школе с 30 000 это будет кошмар. Отчасти поэтому так важно ограничивать социальный контекст.Другой — исключить отношения, которые не имеют значения для вашего исследования. Ограничение или проведение границ означает наличие правила о том, что будет или не будет включено в исследование (⊕Laumann, Marsden, and Prensky 1989Laumann, Edward O, Peter V Marsden, and David Prensky. 1989. «The Проблема спецификации границ в сетевом анализе.» В «Методы исследования в анализе социальных сетей» , под редакцией Линтона С. Фримана, Дугласа Р. Уайта и Антона Кимбалла Ромни, 61–79. Нью-Брансуик: Transaction Publishers.).
Рисунок 3.1: Исследование сети клубов карате Закари было одним из первых проектов по сбору данных в истории СНС. Эти данные известны тем, что показывают, как можно использовать сети для поиска групп на основе отношений между участниками.
Например, если вас интересует, кто с кем дружит в вашем классе социальных сетей, вы привязали свое исследование к просмотру только людей, которые находятся в вашем классе социальных сетей.
Одно из самых известных исследований социальных сетей провел антрополог Уэйн У.Захари (см. рис. 3.1) в клубе карате при колледже в 1970-е годы (⊕Захари, 1977 г. Захари, Уэйн В., 1977 г. «Модель информационного потока для конфликтов и раскола в малых группах». Journal of Anthropological Research 33 (4): 452 –73.). Таким образом, 34 члена клуба карате и внешний учитель были участниками исследования, потому что они были людьми, которые были вовлечены в повседневную деятельность клуба карате на момент сбора данных.
Имея тип социальных отношений в некотором ограниченном контексте, вы можете начать отображать социальный мир в виде графа.В своей самой простой форме граф представляет собой картину отношений между различными типами социальных акторов. Эта картина становится невероятно убедительной, когда мы начинаем использовать математические понятия, чтобы понять, как акторы относятся друг к другу (в основном это то, чему посвящена эта книга) или на каких социальных принципах могла быть сформирована сеть.
Хотя этот класс будет в основном использовать термины «узел» и «ребро» при обращении к графам, это не единственные термины, используемые теми, кто использует методы сетевого анализа.Дополнительные имена для узлов включают вершина или точка . Отношения между двумя узлами, кроме того, что они называются ребрами, называются связями или связями .
| Теория графов | Точка | Строка |
| Сетевые науки | Вершина | Край |
| Социология | Актер | Галстук |
| Информатика | Узел | Ссылка |
Существует несколько более техническое математическое определение графа.
Граф представляет собой набор , обычно представленный заглавной буквой G .
Из курса математики в средней школе вы, возможно, помните, что математическое определение множества — это просто набор сущностей, некоторые из которых могут быть упорядочены, а некоторые сами могут быть другими множествами (множество может иметь множества в качестве своих членов). В случае графов сущности внутри коллекции представляют собой набор из 90 261 вершин 90 262 (также называемых 90 261 узлами 90 262) и отдельный набор из 90 261 ребер 90 262 (также называемый 90 261 ссылками 90 262).
Таким образом, граф представляет собой множество, состоящее из двух множеств: множество узлов (обычно обозначается заглавной буквой V ) и множество ребер (обычно обозначается заглавной буквой E ).
В обозначении теории множеств:
\[\begin{уравнение} G = \{V, Е\} \тег{4.1} \конец{уравнение}\]
Это говорит о том, что члены множества, определенного графом, которое мы называем G , являются двумя другими множествами, называемыми E и V (которые сами имеют ряд элементов внутри).
Обычная запись, как и в уравнении (4.1), состоит в том, чтобы заключить членов множества в квадратных скобках \(\{\}\).
узлов
Набор узлов обычно представляет участников реальной социальной сети. Точечные и линейчатые диаграммы (например, показанные на рис. 3.1) используются для представления графов, которые, в свою очередь, представляют реальную социальную сеть.
На этих диаграммах узлы (представляющие актеров) обычно рисуются в виде круга, но они могут быть любой формы или символа.В анализе социальных сетей действующими лицами часто являются отдельные лица или организации, но, как мы видели, в более широких приложениях сетевых образов в физических и биологических науках (обычно под лозунгом сетевой науки ) узлы могут представляют все, что связано с другими подобными объектами в более крупной системе. К ним относятся электростанции и дома, серверы и компьютеры, животные в экосистеме, города, на самом деле все материальное, с чем мы можем определить какое-то отношение или с помощью которого можно сказать, что происходит обмен определенным типом контента.
Края
Ребрапредставляют собой наличие соединения или социальной связи между двумя узлами. Как мы увидим, это могут быть постоянные отношения (например, «брат») или более мимолетное взаимодействие (например, текстовое сообщение, нахождение в одном и том же месте в одно и то же время). На лекции мы определим, что такое социальные связи, сколько существует типов и каковы их свойства. На данный момент мы можем сказать, что в анализе социальных сетей связи — это отношения или связи между узлами, а ребра в графе предназначены для представления этих связей.
В теории графов набор ребер лучше всего рассматривать как набор из пар узлов, где два члена пары являются узлами, участвующими в социальной связи. Таким образом, если узел A связан с узлом B какой-либо социальной связью (дружба, учебная группа, коллеги), то AB является членом множества ребер соответствующего графа. В нотации теории множеств это обычно записывается как \(AB \in E\), что читается как «ребро AB является членом множества \(E\).
На ребра также можно ссылаться, сопоставляя два узла, которые соединены ребром. Таким образом, ребро AB также можно записать как \(V_A V_B\).
Рисунок 4.1: Простой граф с четырьмя узлами и двумя ребрами.
В случае электростанций и жилых домов края могут представлять собой линии электропередач. Между тем, серверы и компьютеры связаны интернет-кабелями и доступом к Wi-Fi, а города связаны дорогами. Существование краев сигнализирует о возможности передачи контента, будь то мощность, компьютерные данные или люди в автомобилях.В случае социальных сетей контент, который передается между двумя узлами, — это такие вещи, как влияние, советы, информация и поддержка. Но это также может быть болезнь, издевательства или сплетни.
Простые графики
На рис. 4.1 показан пример точечной и линейной сетевой диаграммы графа с четырьмя узлами и двумя ребрами . Узлы A , B , C и D представляют собой круги, представляющие акторов A , B , C и D , чьи социальные отношения в реальном мире нас интересуют.
Линии, проведенные между A и B , а также между B и C , представляют ребра , указывающие на наличие социальной связи. Таким образом, ребра AB и BC появляются на сетевой диаграмме. Отсутствие ребра между узлами B и C отражает отсутствие отношений между субъектами с именами B и C в реальном мире.
Итак, если бы мы расписали график, показанный на рисунке 4.1 с точки зрения множеств, определяющих граф, мы бы сказали:
\[\begin{уравнение} G = \{Е, V\} \тег{4.2} \конец{уравнение}\]
\[\begin{уравнение} Е = \{АВ, АС\} \тег{4.3} \конец{уравнение}\]
\[\begin{уравнение} V = \{А, В, С, D\} \тег{4.4} \конец{уравнение}\]
Это говорит о том, что граф G , показанный на рис. 4.1, представляет собой набор из двух элементов, E и V , каждый из которых представляет собой отдельный набор.
Набор ребер G состоит из двух элементов: AB и AC .Набор узлов G состоит из четырех элементов: A , B , C и D .
У графиков есть несколько основных свойств, о которых нам необходимо узнать:
- В графе, если два узла соединены ребром, они называются смежными . Таким образом, на рисунке 4.1 узлы A и B являются смежными, как и узлы A и C . Пары узлов, которые не связаны ребром, такие как узлы B и C , называются несмежными .
- Узлы на двух концах каждого существующего ребра называются конечными вершинами этого ребра. Каждое ребро имеет две концевые вершины. Как мы уже делали, ребра именуются путем ввода вместе имен их двух конечных вершин. Таким образом, ребро, имеющее узлы A и B в качестве конечных точек, называется AB .
- Если ребро «касается» узла (например, соединяет его с другим узлом), мы говорим, что это ребро инцидентно этому узлу.
Итак, в 4.1, ребро AB инцидентно обоим узлам A и B .11 Соотношение инцидентности будет важно в следующем уроке, когда мы будем обсуждать сетевые метрики, вычисляемые на уровне узла, такие как степень центральности . - Наконец, в графе узлы, которые не связаны ни с какими другими узлами, называются изолятами . Это означает, что в 4.1 узел D является изолятом, поскольку с ним нет инцидентных ребер.
Графики, подобные показанным на рис. 4.1 называются простыми графами . Есть два требования, чтобы граф считался простым графом:
За некоторыми исключениями, упомянутыми в последующих уроках, простые графики могут представлять большинство социальных сетей.
Окрестности узлов
Как мы видели, каждый узел в графе или порядке \(N\), заданном набором \(V = \{v_1, v_2, v_3, \dots v_N\}\), может быть смежным с некоторым набор других узлов.
В теории графов они называются соседями узла . окрестность узла в графе записывается как \(\mathcal{N}(v)\), где \(v\) — имя узла в графе. Например, если мы имеем в виду соседей узла A в графе, показанном на рис. 4.2, мы должны написать \(\mathcal{N}(A)\).
Окрестность каждого узла является собственным подмножеством большего множества узлов в графе \(V\). Это записывается как \(\forall v: \mathcal{N}(v) \subset V\), что переводится с математического на английский как «для всех узлов \(v\) окрестность \(v\) равна подмножество большего набора узлов \(V\).Например, на рис. 4.2 \(\mathcal{N}(A) = \{B, C, D, F\}\) и \(\mathcal{N}(A) \subset V\)33. Математический символ подмножества — \(\подмножество\).
Рисунок 4.2: Еще один простой график.
Пересечение соседства узлов
Обратите внимание, что наборы соседей двух узлов могут иметь общие элементы. Например, на рис. 4.2 мы имеем \(\mathcal{N}(A) = \{B, C, D, F\}\), а также имеем \(\mathcal{N}(D) = \{A , В, F\}\).
Эти два набора имеют общие члены!
Иногда нас может интересовать общее количество других людей, с которыми два узла имеют общее соединение.Например, когда вы задаетесь вопросом, со сколькими людьми вы и ваш друг дружите (или алгоритм социальных сетей позволяет вам узнать). Это называется пересечением двух наборов соседства узлов.
Таким образом, если A и D оба являются узлами в графе, пересечение их наборов соседства дает нам список других узлов в графе, к которым они оба подключены . Используя нотацию теории множеств, это можно записать как: \(\mathcal{N}(A) \cap \mathcal{N}(D) = \{B, F\}\), что говорит о том, что узлы A и D имеют B и F в качестве общих соседей.44 Математический символ для пересечения множества — \(\cap\).
Мощность множеств, образованных пересечением окрестностей всех узлов графа, дает нам число общих соседей , которое может быть равно нулю, если два множества окрестностей не пересекаются .
55 В теории множеств кардинальность 90 262 набора — это количество элементов в этом наборе. Таким образом, мощность множества \(\{A, B, C, D\}\) равна четырем. В теории графов два множества называются непересекающимися, если они не имеют общих элементов.В следующем уроке мы увидим, что эта величина имеет приложения для получения важных матриц из графиков и вычисления некоторых ключевых сетевых метрик в сети.
Обратите внимание, что два узла могут иметь общих соседей, даже если они не связаны напрямую в сети! Таким образом, количество общих соседей определяется для и связанных и нулевых диад.
Например, на рис. 4.2 пересечение окрестностей узлов D и E существует и задается выражением \(\mathcal{N}(D) \cap \mathcal{N}(E) = \ {B, F\}\), хотя узлы D и E не связаны (несмежны).
Союз соседства узлов
Иногда нас может интересовать общее количество других людей, к которым подключены два узла, независимо от того, подключены ли они оба к ним.
Думайте об этом как о добавлении набора людей, которых вы знаете, к набору людей, которых знает один из ваших друзей, считая людей, которых знает ваш друг, но не знаете вы, и людей, которых вы знаете, но не знает ваш друг. Это называется объединением двух наборов соседства узлов.
Итак, если A и D оба являются узлами в графе, объединение их наборов окрестностей дает нам список общего числа других узлов в графе, каждый из которых связан с .
Используя нотацию теории множеств, это можно записать как:66 Математический символ для объединения множеств — \(\cup\).
\[\begin{уравнение*} \mathcal{N}(A) \cup \mathcal{N}(D) = \{B, C, F\} \конец{уравнение*}\]
В котором говорится, что узлы A и D имеют B C и F в качестве соседей, но не обязательно общих соседей.
Как мы увидим позже, пересечение и объединение множеств соседства можно использовать в качестве основы для построения мер (структурного) сходства между узлами графа.
В графе степень данного узла можно определить двумя способами, оба из которых приводят к одному и тому же ответу.
Один из способов представить степень данного узла \(i\) в графе (обозначается как \(k_i\)) — это мощность набора соседей этого узла, как определено ранее:
\[\begin{уравнение} k_i = |\mathcal{N}(i)| \тег{5.1} \конец{уравнение}\]
Итак, на графике, показанном на рис. 4.2, \(k_A = |\mathcal{N}(A)| = |\{B, C, D, F\}|=4\).
Другой способ представить степень узла — это не количество элементов множества окрестностей узлов, а количество ребер . В этом случае мы подсчитываем количество ребер, имеющих данный узел \(i\) в качестве одной из своих конечных точек. Напомним, что ребро, которое имеет данный узел в качестве одной из своих конечных точек, называется инцидентным этому узлу. Таким образом, в графе, показанном на рис. 4.2, множество ребер, имеющих узел A в качестве одной из своих конечных точек, равно \(k_A = \{AB, AC, AD, AF\}\) и \(|k_A|\) = 4.
. В любом случае, вычисление степени как мощности множества соседей узла или как количества ребер, инцидентных узлу, дает нам количество других участников, с которыми данный узел связан в сети.77 Мы увидим позже. Урок, что это важная мера положения узла, называемая центральностью градусов .
Рассмотрим график, показанный на рис. 4.2. Если сюда включены все актеры, которых вы хотите изучить, мы будем называть их всей сетью .Однако иногда, даже когда мы собираем данные о большом количестве акторов, нам может быть интересно проанализировать не всю сеть, а только некоторые ее части. Как мы это делаем?
Рисунок 6.1: Подграф неориентированного графа
Что ж, хорошо, что граф на самом деле представляет собой множество из двух множеств. Если вы помните школьную теорию множеств, вы всегда можете взять множество и рассмотреть только 90 261 подмножество 90 262 исходных элементов.
Поскольку графы являются множествами, мы можем сделать то же самое.
Подмножество исходных узлов (или ребер) графа называется подграфом . Итак, если \(G =\{E,V\}\) — исходный граф, то подграф \(G’ = \{E’,V’\}\) является подмножеством \(G\), т.е. пишется \(G \подмножество G’\), имея в виду, что \(E’ \подмножество E\) и \(V’ \подмножество V\).
Рисунок 6.2: Другой подграф неориентированного графа
Например, предположим, что нас интересует только анализ актеров A , B , D и F на графике, показанном на рисунке 4.2. Они кажутся сплоченной группой людей. В этом случае, как отмечалось ранее, если мы назовем исходный граф \(G\) с множествами вершин и ребер \(\{E, V\}\), мы можем определить новый подграф \(G’\), узел которого подмножество \(V’\) включает только интересующих нас акторов, в данном случае \(V’ = \{A, B, D, F\}\), где \(V’ \подмножество V\).
Подграф \(G’\) показан на рис. 6.1. Это выглядит именно так, как мы хотели, фиксируя отношения между взаимосвязанной подгруппой акторов в исходном графе.
Обратите внимание, что набор ребер подграфа \(E’\) включает только те ребра, которые инцидентны другим узлам в подграфе, и опускает те ребра исходного графа, которые соединяются с узлами, не входящими в подграф, поэтому \(E ‘ \subset E\).88 Как мы увидим позже, хорошо связанные подгруппы акторов исходного графа называются связным подмножеством .
Подграфы, индуцированные вершинами и ребрами
Для любого графа мы можем определить подграф на основе любого старого случайного подмножества исходного набора узлов.Это полностью зависит от нас. Например, мы могли бы определить новый подграф \(G»\) исходного графа, показанного на рис. 4.2, который включает набор узлов \(V» = \{C, E, F\}\). Это показано на рисунке 6.2. Этот подграф странный и, вероятно, не очень полезный, но в любом случае это подграф исходного графа!
Точно так же, как мы можем определять подграфы на основе набора узлов графа, мы можем определять подграфы на основе подмножеств исходного набора ребер.
Например, мы могли бы выбрать ребра \(E’ = \{AB, AC, AF\}\) и определить на их основе подграф, который обязательно будет включать множество узлов \(V’ = \{A, B, C , Ф\}\).
Рисунок 6.3: Еще один подграф неориентированного графа
Когда подграф определяется путем выбора подмножества узлов для сохранения (общий случай), он называется индуцированным узлами подграфом исходного графа. Когда подграф определяется путем выбора подмножества ребер из исходного графа для сохранения, он называется (как вы уже догадались) подграфом , индуцированным ребрами исходного графа.
Подграфы с удаленными вершинами и ребрами
Обычная причина для определения подграфов в анализе социальных сетей — когда мы задаемся вопросом, как будет выглядеть сеть, если нужно избавиться от актера или галстука.Иногда это полезно, когда мы хотим понять, насколько важен актер для удержания сети вместе. Таким образом, можно определить подграф, удалив узел (или ребро).
Это записывается \(G’ = G — i\), где i — имя узла, который мы удаляем. Итак, это говорит: «Дайте мне подграф G’ , который равен исходному графу G минус вершина i ».
Например, на рис. 6.3 показан подграф, который получается, когда мы удаляем узел A из графа на рис. 4.2: \(G’ = G-A\). Это называется подграфом с удаленными вершинами исходного графа.
Подграфы также можно получить, выбрав более одного узла из исходного графа для удаления. Подграф, полученный в результате удаления 90 251 всех 90 252 узлов исходного графа (так, что мощность набора ребер теперь равна нулю), называется 90 261 нулевым графом 90 262 . Подграф, который получается в результате удаления всех узлов исходного графа , кроме для одного (так, чтобы множество узлов полученного подграфа включало только один узел), называется одноэлементным графом (один действительно одинокое число в социальных сетях ).
Рисунок 6.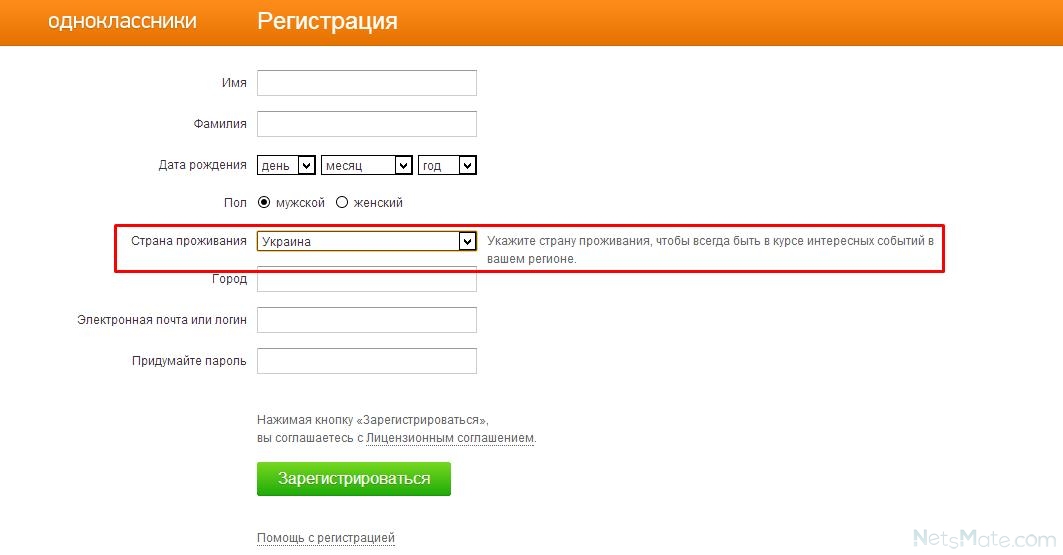
4: Еще один подграф неориентированного графа
Если бы мы определили подграф, удалив вместо этого одно ребро, то он был бы назван подграфом с удаленным ребром исходного графа. Например, подграф, полученный в результате удаления ребра \(AB\) с рис. 4.2, записанный как \(G’ = G — AB\), показан на рис. 6.4.
Как и в случае с узлами, подграфы также могут быть получены путем удаления одновременно более чем одного ребра. Подграф, полученный в результате удаления всех ребер в графе, так что мощность множества ребер становится равной нулю, называется пустым графом.
Как мы увидим позже, подграфы (а также удаление вершин и ребер) являются полезной концепцией для обсуждения уровней на «промежуточных» уровнях, выше уровня узла, но «ниже» уровня всей сети: подгруппы. Однако подграфы также полезны для сетевых концепций на уровне узла, потому что существует особый тип подграфа, называемый эго-графом , который определяется путем выбора центрального узла и узлов, связанных с ним.
Популярный веб-сайт социальной сети
А как насчет вашего сторонника, которого вы потеряли и делаете новых, что может быть лучше этого?
вы даже будете готовы возобновить старые дружеские отношения или завести новые.Воссоединение вместе со своими старыми друзьями
Присоединившись к Одноклассникам, вы можете быть готовы не только к установлению контакта со своими старыми одноклассниками и друзьями, но и к доскам объявлений
.
объявлений всем, с кем вы только что посещали школу. Платное членство также дает вам возможность использовать
только для индивидуальной связи со своими одноклассниками, но вы также сможете направлять широковещательные сообщения или упомянутые
, это членство сравнительно легко себе позволить. Как только вы станете платным участником, вы не сможете связаться с людьми, с которыми вы потеряли связь, вам придется стать платным участником.Как и раньше
Хотя вы сможете просматривать профили других участников с бесплатным членством, вы не можете связаться с ними.
для создания
информации о ваших одноклассниках. 90 812 присутствовали. это означает, что вне зависимости от того, закончили ли вы обучение в 1970 или 2000 году, вы должны быть готовы к тому, чтобы получить 90 812 всех по категориям. Эти категории включают не только колледжи, которые посещал каждый, но и годы, в течение которых 90 812 профили других участников, особенно тех, с кем вы посещали школу, легко. Одноклассники разделили
Благодаря бесплатному членству вы сможете публиковать свой собственный профиль и просматривать профили других участников.Просматриваете веб-сайт
? однако, как только вы официально станете участником, вы добавите дополнительную информацию в свой профиль.
выполнено, вам нужно будет создать профиль пользователя. Этот профиль является частью того, что будет отображаться на
www.classmates.com. Оказавшись на их главной странице, вы увидите метод выбора школы. Если у вас есть 90 812. Если вам интересно посмотреть, что могут предложить Classmates, вы легко это сделаете, посетив их онлайн-сайт за 90 812 долларов в месяц.
по карману.В настоящее время существует три разных уровня членства, на которые вы можете просто подписаться, лучший из которых должен предлагать только пять
, это того стоит. Кроме того, членский взнос, чтобы быть выгодным, напрямую связан с
позиционированием. Несмотря на тот факт, что вам просто нужно стать платным участником, чтобы пользоваться платным членством Classmates
. есть бесплатный план членства, который доступен, но вы ограничены тем, что вы сможете делать на
сайт стоит присоединиться.
, вы можете связаться практически с кем угодно на сайте. это одна из многочисленных функций Classmates
школы, старшей школы или колледжа. Хотя рекомендуется, чтобы вы просто связывались с теми, кого вы узнаете из 90 812 других. это может быть связано с тем, что одноклассники сосредотачиваются на связях, которые были установлены в классе, независимо от того, является ли это основной
или нет.
, чтобы знать. если только вы не присоединитесь к одной из самых популярных социальных сетей в Интернете.